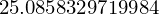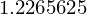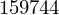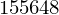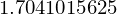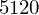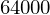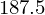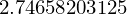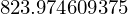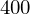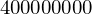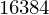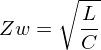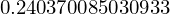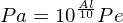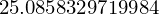(School) ~ Mathe SA Vorbereitung

import sympy as sp
sp.init_printing()

1)

    1256 Byte     --> KiB
    156 KiB       --> Byte
    152 Mebibyte  --> KiB
    1745 Gibibyte --> Tebibyte
    5 Tebibyte    --> GiB

MB ==> Megabyte ==> 1000

MiB ==> Mebibyte == > 1024

B -> KB -> MB -> GB -> TB -> PB

a = 1256 # Byte
a / 1024

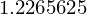
1.2265625

a = 156 # KiB
a * 1024

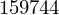
159744

a = 152 # MiB
a * 1024

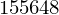
155648

a = 1745 # GiB
a / 1024

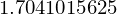
1.7041015625

a = 5 # TiB
a * 1024

5120

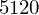
2)

Berechne Speichergröße

    Auflösung (w x h): 320 x 200
    Farbtiefe:         24 bit
    Bilder/Sekunde:    15 Bilder
    Laufzeit:          5 Minuten

Gesucht:

Gesamtzahl der Bildpunkte (Auflösung)
Speicherbedarf für 1 Bild in Kibibyte
Speicherbedarf pro Sekunde in Mebibyte
Gesamt -speicherbedarf in Mebibyte

Auflösung = 320 * 200
Auflösung

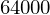
64000

Bild = (Auflösung * 24) /8 / 1024
Bild # Kibibyte

187.5

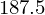
Sekunde = Bild * 15 / 1024
Sekunde # Mebibyte

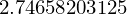
2.74658203125

Gesamt = Sekunde * 60 * 5
Gesamt # Mebibyte

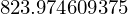
823.974609375

3)

Berechne Anzahl der übertragenen Bits nach Übertragungszeit von 4 Sekunden bei 100 MBit/s Leitung?

100 * 4 # MBit :O

400

_ * 1000 * 1000 # Bit

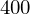
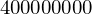
400000000

4)

Datei mit 2 GiB soll zum Server, 6 Mbit/s. Wie lang dauerts? (mm:ss)

# vlt genauer?
#x = 2 * 1024 # GiB --> MiB
#x = x * 1024 # MiB --> KiB
#x = x * 1024 # KiB --> Byte
#x = x * 8 # Byte --> Bit
#x = x / 1000 # Bit --> KBit
#x = x / 1000 # KBit --> MBit
x = 2 * 1024 # GiB --> MiB
x = x * 8 # MiB --> MBit
x

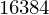
16384

seconds = x / 6 # 6 Mbit/s
minutes = sp.floor(seconds / 60);
seconds = sp.floor(seconds % 60);
print("%s:%s" % (minutes, seconds))

45:30

6)

zweiadriges Kabel, Länge 5,6 km, folgende Kenngrößen

R = 1100 Ohm
L = 4,24 mH
C = 205,2 nF
G = 0,77 microS

Wie groß sind die Leitungswerte des Kabels?

Klingt Wie “Du hast 3 Äpfel, Peter hat 2, Wie schnell dreht sich die Erde um die Sonne?”

7)

Wie groß ist der Wellenwiderstand einer Leitung, die einen Kapazitätskennwert von 45 pF/m und einen Induktionskennwert von 2,6 mirćroH/m hat?

Formel:

Zw = sqrt(L’/C’)

    Zw ==> Wellenwiderstand einer Leitung
    L' ==> längenbezogene Induktivität
    C' ==> längenbezogene Kapazität

Zw, L, C = sp.symbols('Zw L C')

f = sp.Eq(Zw, sp.sqrt(L/C))
f

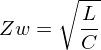
$Zw = \sqrt{\frac{L}{C}}$

sp.solve(f.subs({C:45, L:2.6}))[0] # Ohm ?

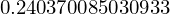
0.240370085030933

8)

Das Koaxialkabel RG 58 hat eine Dämpfung von -12 dB/100m. Die Eingangsleitung beträgt Pe = 1 mW

Wie groß ist die Ausgangsleistung nach 40 Meter?
Nach vievielen Metern ist die Ausgangsleitung nur mehr die Hälfte der Eingangsleistung?

Logarithmus

y = 2x | logarithmieren

log2y = x

There are several conflicting meanings associated with the notation lgx. In German and Russian literature, the notation lgx is used to mean the common logarithm log_(10)x. This is also the usage recommended by the United States Department of Commerce (Taylor 1995, p. 33).

However, lgx is sometimes identified with the binary logarithm log_2x in some number theoretic literature (and here, log_2x mean the base-2 logarithm, not the nested natural logarithm log_2x=lnlnx as defined by Ivić 2003).

Great care is therefore needed to determine the intended definition for lgx when it is encountered in the wild.

Formeln lt Buch:

Al = 10lg(Pe/Pa)dBm

Umgewandelt:

**Pa = 10^((A/10)l)Pe

    l ==> Länge des Kabels
    A ==> Dämpfungsausmaß in dB
    a ==> Dämpfungskoeffizient in dB/km
    Pe ==> Eingangsleistung
    Pa ==> Ausgangsleistung

Pe, Pa, A, l = sp.symbols('Pe Pa A l')

f1 = sp.Eq(Pa, 10**((A/10)*l) * Pe)
f1

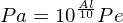
$Pa = 10^{\frac{A l}{10}} Pe$

sp.solve(f1.subs({Pe:1, A:(-12/100), l:40}))[0] # mW

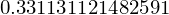
0.331131121482591

sp.solve(f1.subs({Pe:1, Pa:0.5, A:(-12/100)}))[0] # länge

25.0858329719984